물리 개념
벡터:크기랑 방향을 모두 다 가지고 있는것.
벡터에서 크기:화살표의 길이.
[벡터]:벡터의 크기.
벡터 성질 방향과 크기만 같으면 같은 벡터
cos의 역함수 arccos
내적 벡터의 곱(.)
증명1
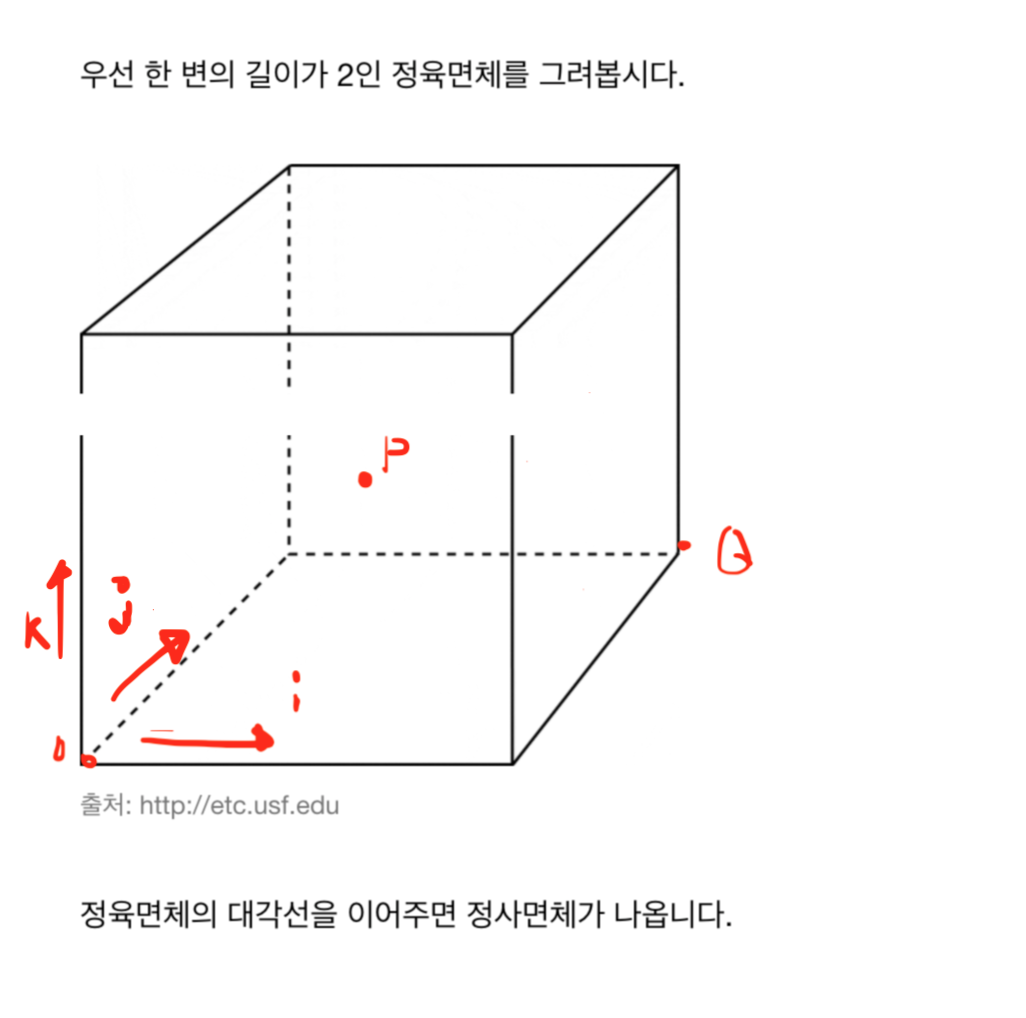
왼쪽 아래 끝의 꼭짓점을 원점 O라고 가정하고, 정육면체의 중심을 P, 그리고 또 다른 정사면체의 꼭짓점을 Q 라고 합시다.
정육면체의 중심은 정사면체의 중심과 동일하며, 탄소의 위치를 나타냅니다.
오른쪽으로의 방향을 i, 화면 안으로의 방향을 j, 위로의 방향을 k 라고 가정합시다.
정육면체 한 변의 길이는 2라고 가정합니다.
메탄은 정사면체 구조를 가지고 있습니다.
수소 원자를 서로 이어주면, 수소 원자를 꼭짓점으로 한 정사면체가 나옵니다. 탄소는 그 중심에 있습니다.메탄의 H-C-H 결합각은 약 109.5o 입니다. 이 각도는 정사면체의 한 꼭짓점-중심-꼭짓점의 각도와 동일합니다.이것은 벡터를 이용하여 간단하게 증명할 수 있습니다.
우선 한 변의 길이가 2인 정육면체를 그리고 정육면체의 대각선을 이어주면 정사면체가 나옵니다. 왼쪽 아래 끝의 꼭짓점을 원점 O라고 가정하고, 정육면체의 중심을 P, 그리고 또 다른 정사면체의 꼭짓점을 Q 라고 합시다.
정육면체의 중심은 정사면체의 중심과 동일하며, 탄소의 위치를 나타냅니다.
오른쪽으로의 방향을 i, 화면 안으로의 방향을 j, 위로의 방향을 k 라고 가정합시다.
정육면체 한 변의 길이는 2라고 가정합니다.
점 P 는 정육면체의 중심이므로 벡터 OP 는 i + j + k 입니다.
벡터 OQ 는 2i + 2j 입니다.
따라서,
PO = - i - j - k
PQ = i + j - k
이제 두 벡터의 내적을 구합시다.
PO . PQ = - 1 - 1 + 1 = -1
그리고,
| PO | = √(3) | PQ | = √(3) 이므로 각 OPQ = x 에 대하여
cos x = (PO . PQ) / ( |PO| |PQ| )= -1 / 3
따라서, x = arccos(-1/3) = 109.47122....≈ 109.5˚
증명 2

메테인에 대해
메테인(Methane 메세인, CH4) 또는 메탄(Methan)은 가장 간단한 탄소 화합물로, 탄소 하나에 수소 4개가 붙어 있다. 분자량은 16이다. 녹는점은 -183 °C, 끓는점은 -162°C로 상온에서 기체이다.
자연적으로는 유기물이 물 속에서 부패, 발효할 때 생기므로 늪지대의 바닥 등에서 발생한다. 또 석탄층 속에 함유되어 석탄갱내에서 발생하여 공기와 섞여 폭발을 일으킬 때도 있다. 천연 가스나 석탄 가스의 주성분을 이룬다.
C-H의 결합 길이는 0.110nm이며, C-H의 결합 사이의 결합각은 109.5°이며, 무극성 분자이다.
순수한 메테인은 냄새가 없으나, 산업용으로 사용할 때 누출 여부 확인을 위해 냄새가 나는 다른 화합물을 일부 첨가하여 판매한다.
천연 가스의 주성분으로, 연료로 많이 사용된다. 메탄 분자 하나를 태우면 이산화 탄소 한 분자와 물 두 분자가 생성된다. 반응식은 다음과 같다.
CH4 + 2O2 → CO2 + 2H2O
'정보 관련 포스팅 > 과학' 카테고리의 다른 글
| dna 구조 발견의 역사 보고서 (4) | 2021.11.27 |
|---|---|
| 토머스 쿤, 패러다임 (4) | 2021.11.25 |
| 초고층 빌딩의 안정성을 보장하기 위한 설계에 대한 것들 (0) | 2021.11.19 |
| Atomic Theory and Structure(원자이론과 구조) (0) | 2021.11.18 |
| 빌 게이츠 방사능에 대한 연구,후쿠시마 오염수 방류에 대한 정리 (0) | 2021.11.17 |
